File: 1484092942213.jpg (67.41 KB, 398x537, 1477841256001.jpg)

No. 231026
I'm not sure if this belongs here, but I've been seeing this guy pop up a lot on /r9k/; maybe someone here has some information etc.
His name is Oscar and he is from Stockholm, Sweden. He sometimes goes by the name Eric and has also been saying that he is from Germany.
He is 25 years old, a NEET and spends his time on lifting and being obsessed with mentally ill girls. He also enjoys anime a lot.
He baits them with his 'mysterious' behaviour, manipulates them before they eventually send him nudes. Some say he also meets up for sex before then turning on them, insulting them and then fucking off.
Here's an archived thread with a lot of pictures of him and some (anecdotal) statements where he posts aswell (with confirmation picture):
https://desuarchive.org/r9k/thread/32420752/And a few logs he had with PoisonIvyLul:
http://desuarchive.org/r9k/thread/32309506/ Sadly no social media links because he seems to be pretty careful about that stuff.
No. 231056
>>231040Not a self post actually. I talked to him last year for a while and only recently found out that he preys on online girls and exploits them.
I just find it weird because apparently he has done it to so many, yet there's hardly any information on him really.
>>231046What does he like/how did he come across?
What did he usually say?
No. 231086
File: 1484098313953.jpg (42.65 KB, 388x844, 1477841103876.jpg)

>>231063Either that or names of girls
No. 231093
i dont think its a self post because this guy tries to stay under the radar. but yeah he is fucking mental, but hard to observe because he tries hard not to get caught
he still posts on r9k every day, he will post his skype in almost every thread where he can attempt to contact a female. if he look through the archive under "skype" half of the posts link back to his usernames. he switches between a variety of them, usually random digits like s9484.894 for example. i reckon he probably has dozens of different ones.
honestly hes a creepy fuck and if i had more time i'd use this thread to compile all of his skype/discord shitposts just to spook him
No. 231097
>>231086Holy hell this dude is an uggo. How does he get anyone to fall for him? Like, I mean… I can understand stupid teens falling for Onion boy but this has me confused
>>231093oh anon if you find the time, please do. people like this guy are scumbags who deserve to be unhappy
No. 231102
File: 1484099283843.jpg (33.75 KB, 290x293, 1477842752945.jpg)

>>231093Yes, exactly. I enjoyed talking to him a lot bck then, I have to admit, but he got very clingy and very pushy for sexual stuff, so I just stopped talking to him.
A few days ago a girl posted on /r9k/ that she had a crush on a robot and it turned out to be him and the thread kind of exploded and a lot of people posted information etc.
I was surprised to see that he is STILL doing this. I would feel bad for him if he weren't knowingly/willingly doing this.
I agree with
>>231097 though, you really should post more information.
Pic related, he uses this a lot aswell (same bathroom.)
No. 231115
File: 1484100159130.jpg (16.22 KB, 216x211, 1477842617585.jpg)

>>231110Yeah. He was involved in the PoisonIvyLul stuff and she leaked the two pictures posted above; if you reverse search them it's not only the Daily Mail that posted them. I would feel like killing myself to be honest.
This is the last picture I have of him, but they're all at least 3-4 months old.
No. 231119
>>231026i heard that he is trying to "fill a void" that he has now due to an ex girlfriend leaving him/betraying him before all this. some say that that is why he is like he is.
does anyone have any information about that?
i only know that he was in an "online relationship" with a tripfag on r9k called mystery.jpg, but once he found out that she had cheated on him he leaked all the sexual content he had of her (nudes and even masturbation videos.)
No. 231130
>>231122Yeah, I would be very careful. He has been telling some girls that he is a virgin lmfao, but telling others that he's not. It's quite obvious that he has had his fair share with girls though.
>>231121>>231125The worst thing is that he hasn't properly been caught yet. I've been trying to find more information, but this is all I am able to get since he uses different names, locations, personas, Skype accounts and is a manipulator in general. He lies A LOT and I'm actually fucking gobsmacked that he's still doing this even though his face is already plastered over news sites all over the world.
No. 231135
>>231093i am not this person, but i know that luuweil@outlook.com is one of his accounts that he uses.
here are some threads where he posted his contact information in. his writing style is very recognizable if you know it.
just ctrl + f for "luuweil":
http://randomarchive.com/board/b/thread/715166069 - fetish thread
https://yuki.la/soc/24617493 - contacting someone in a looking for gf/bf thread
https://yuki.la/soc/24648458 - another contact thread where he contacted a girl
https://desuarchive.org/r9k/thread/32156929/ - aaaand another contact thread for a bf
No. 236098
File: 1484670831183.jpg (165.69 KB, 1866x888, 7861 hrs Dota 2 LMAO.jpg)
Here, I made you all a huge pastebin. Enjoy.
http://pastebin.com/xLgvngHR>>231121They have and if you want more you can message me to talk about it. He is vile.
No. 236716
File: 1484769676112.jpg (37.36 KB, 268x373, 9364237542356.jpg)

>>236507do you have any information or even pictures of him still? i was not around then, but he just keeps on pumping and dumping these females.
No. 236793
File: 1484775587066.jpg (93.84 KB, 405x654, 420387529835632.jpg)

>>236720Apparently he only owns this pair of briefs
No. 236829
File: 1484779056859.jpg (25.79 KB, 480x384, CIDTNIjWoAEzS3U.jpg)

>>231086This is what I thought of.
Anyway he'd be alright looking if he got rid of that fucking fried toupee looking hairstyle
No. 236934
>>236878stuff from there is so rare cus that weird shotacon chick kept pw locking the chat
There was a picture of him afking and then someone in the chat says they like chocolate or something and he took a picture holding chocolate infront of the chat on his screen and posted it not even typing a word this whole time
No. 237025
>>236720>>236829lmfao!
>>236793its the only pair he owns that doesnt have anime characters on them.
No. 238050
File: 1485046752497.png (1.03 MB, 721x681, 1484103420211.png)

>>236934>>236507>>236878>>237037>>237318>>237410do you guys have any more information about him ? he seems to lie a lot about himself and his life and says w/e the other person would like to hear (or what he thinks they would like to hear)
i can confirm the sadboys liking and i have read a lot about him fantasizing about being humiliated, tortured and so on too
why did he leave ? what kind of "mental breakdown" did he have ?
>>236993how did you two get in contact ? thread on r9k ? if so what was it about ? he seems to lurk in fetish threads, looking for gf threads or attention seeking fembot threads
>>236815he has been sending this video to a few females
if anyone has some information or maybe even has spoken to him then post it here or contact the person
>>236098 which also contains most information on this 'man'
it is sad that someone nearly being 27 y/o wastes their life like this
No. 238054
File: 1485047181567.png (411.22 KB, 522x553, tumblr_ntlpy0jnaC1ud7sn6o1_540…)

>>231026oh shit oh shit oh shit i dated him
No. 238055
File: 1485047318227.png (467.61 KB, 409x583, 22.png)

>>238054do you want to talk ? i have information and i am curious what you know
No. 238077
File: 1485052240308.png (434.19 KB, 700x635, 55.png)

>>238073he seems to be very bad at taking pictures
i agree though, the hair is a strange crossbreed of justin bieber, anime protagonist and mom tried cutting my hair
No. 238090
File: 1485054772948.jpg (35.47 KB, 477x666, 1484772911482.jpg)

>>238088cute and all until he comes and tries to impress you with his pissy knife
No. 238092
>>238090like i said, autist
as are all of the girls that talked him
No. 238097
File: 1485056214057.jpg (24.03 KB, 258x260, 1484772519992.jpg)

>>238095to be fair oscar will go after any human with female anatomy (and male if he feels like it)
he seems to have a scheme of prey that he goes after: insecure, scared, lonely, clingy and even mentally ill but probably wouldnt exclude other girls if he had the chance
pretty much will take whatever he can get
No. 238409
>>238050Wow, he is so ugly. no wonder he does this shit…
He added me on skype before too, and we didn't talk much. i deleted him a week later because i do that when i dont talk to people, and then he kept adding me on different accounts to harass me
i didn't know he was this fugly though, whats wrong with his face…?
No. 238451
File: 1485118423391.png (350 KB, 288x712, 44.png)

>>238410>>238409he tries to make up with his body i guess hahahah
No. 238455
>>231086lol, I saw this on the Poison Ivy thread and thought what is this guy doing here with the fat ungroomed autists?
His decent appearance must trick girls. Or makes them tolerate his creepy desperate autistic ass.
No. 238466
File: 1485119871027.png (82.3 KB, 230x147, 33.png)

>>238455compared to how most guys from 4chan / r9k look he does look decent
he also likes anime and other stuff that a lot of girls tend to like
some girls just fall for it all very hard and others find it disgusting
No. 238801
File: 1485183250176.png (56.78 KB, 1141x422, oscar.png)

>>238768Most of the pictures (and the video) he uses seem to be pretty old
>>238778He tells that most girls, probably to make them feel special and to somewhat reinforce his 'autistic, lonely, awkward' persona he puts on
Picture added is an extract from the logs with PoisonIvyLul from when he talked to her last year. Gives a little insight into the mind of Oscar.
No. 238841
>>231026Oh yeah. As a dude that takes advantage of being a blue-eyed confused bumbling nerd I always wondered if someone like this existed.
Just industrially taking advantage of your sperglord detachment to pull this ugly strategy where you just run through girls and are able to rapidly drop the ones that won't fall for it long enough because of the inherent creepiness of it all - like a Nigeria letter where you put the bar low so only really stupid people respond - and then always avoiding blame partially because "surely, he couldn't have done that, he's utterly inept" and partially because of social vagabondage - if you're a true NEET then it doesn't matter anyway, nothing stops you from leading an entirely predatory social life.
It kind of reminds me of Appelbaum from the Tor project. But he got caught because he stuck around a given social circle i guess. If this guy has no ties he's immune to social censure and as long as he avoids technically breaking any laws he'll face no consequences whatsoever.
<tinyboard ban message></tinyboard>
No. 238913
File: 1485203465097.png (31.29 KB, 1064x752, 1484267843915.png)
>>238910There's even more
No. 238933
File: 1485209958875.png (3.91 KB, 509x146, 1484267596529.png)
>>238929He also has some things he says quite often like "Wowie; Huh; Weirdo; Ha; Calm down". He hardly ever uses emoticons. It's not hard to recognize him if he doesn't try to change his style.
He feels very bitter towards "normies".
No. 238945
>>238913He is retarded and ugly.
Did this alice girl take him back?
No. 238947
File: 1485211472561.png (529.64 KB, 1502x1240, Screen Shot 2017-01-23 at 5.43…)
Found some chatlogs he's in on /r9k/
No. 238948
File: 1485211499790.png (82.24 KB, 1335x994, 1485116421395.png)
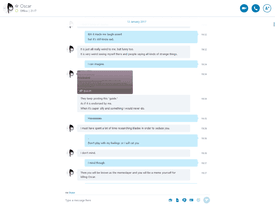
>>238947He is really cringe & so is his obsession with bladee
No. 238949
File: 1485211527293.jpg (93.4 KB, 762x416, 1485117912134.jpg)
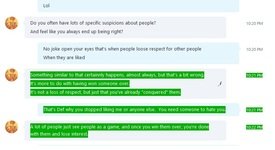
>>238948A look into his sick mindset
No. 238950
>>238945No, she posted a bit about him in this thread if anyone wants to read about it
https://desuarchive.org/r9k/thread/34092704/#34099818"More. He also thinks he looks like Eren from Attack on Titan." kek
No. 238951
File: 1485211549390.png (53.03 KB, 1335x890, 1485117960793.png)
>>238949Him admitting he's autistic basically
No. 238952
File: 1485211737974.png (83.91 KB, 256x256, 57822c19e1ad1.png)

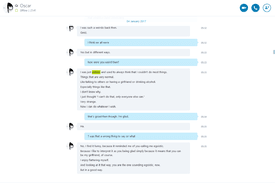
>>238951>Because I like to interpret it as you being glad simply because it means that you can be my girlfriend, of course.MY FUCKING SIDES
No. 238958
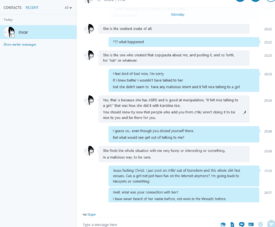
>>238953They were on a 4chan.org/r9k thread for Oscar, some girl posted them claiming she was catfishing him. She is the blue bubbles and he is the grey ones.
I'm posting them because I think they're interesting
No. 238961
File: 1485212982617.png (47.16 KB, 853x940, Untitled1.png)
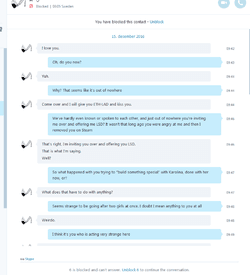
>>238953I'm not sure who is posting those (if it's anyone directly involved with this) but they took them from the thread I made on /r9k/ the other day. I'm the one who made the pastebin here
>>236098 and have spoken with Oscar as well as a few other girls who have. I'll adopt a temporary trip just so it's clear what I post since I'm so involved with this rubbish, I've only made a couple of posts in this thread.
https://desuarchive.org/r9k/thread/34340359/I first openly posted much of anything about him in a thread in October. I called out him posting and posted a paragraph describing him (which interestingly someone has gone and been posting around since then, who Oscar thinks is me but isn't).
https://desuarchive.org/r9k/thread/32420752/#32421545That caused talk of him to increase a lot, and then the past week or so there's been all this other stuff which has given him even more attention that he's not happy about. I have more info such as dox of his address, mother and brother's phone numbers, etc, that I haven't posted.
Here's part of a really pathetic conversation I had with him as proof.
>>238947I'm who he's talking about here, and he was trying to get her to stop talking to me, because stuff I was saying about him was true and she stopped falling for his manipulation.
No. 238962
File: 1485213042521.png (54.37 KB, 818x820, Untitled2.png)
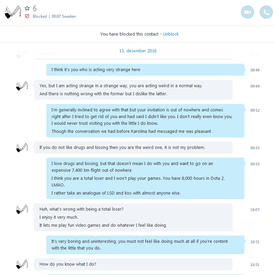
>>238961>Oscar enjoys being a total loserlmao
No. 238981
File: 1485216147939.png (1.57 MB, 1903x3304, https___soundcloud.com_tt1080p…)
>>238976Not sure where in that thread it said we were catfishing him, we haven't been. I did something like that once, but that was it. He's absolutely paranoid of me and so it's really hard to do stuff like that, he thinks some people who legitimately aren't me, are me, and looks for me all over. Probably has a collection of info from stalking (of posts and stuff that may or may not be me).
I've spoken to him several times and gotten a lot of real info. I don't think he's likely to wittingly have a conversation with me again. It's interesting seeing how he interacts with different people. Though I don't think there's too much more for me to learn but you never know. It would be fun to talk to someone else who had dealt with him and see what their conversations were like.
I sent him screenshots on one of his Skype accounts I had added from Google street view of where he lives and threatening to call his mother if he doesn't behave, but he never replied.
>>238977He told me that was just from "leaving it on all night" over and over and not legit hours, I told him I sure hope so. I heard from someone else that he's bragged about 6000+ hours in it though lmao, so I think probably 1/3 of his time since 2013 actually has been Dota. Then the rest anime, masturbation (which is no doubt most of his sexual experience), and going after girls on /r9k/ and lolcow.
No. 252399
File: 1487207815863.png (1.08 MB, 992x1435, oscar.png)

>>236815I talked to him a long time ago
Some time last year he also sent me this video, so it is not recent
I screencapped three frames to help others identify him
Rotated for better visability
No. 252406
File: 1487208475827.png (1.83 MB, 814x1080, oscar-1.png)

https://gfycat.com/FatOptimalGeladathis video was sent to a female from oscar not too long ago (end of january this year). the sound is missing, but it just was a slight static noise and the noise of him dropping his phone.
he had contacted the female in a /r9k/ thread which topic was about sexually dominant women.
oscar often sends
>>231102 this body picture to "introduce" himself and show off. if females state their doubt or want a time stamp then he records a video of him presenting his body (only ever showing the lower part of his face) and recording the recent skype history - like he did in the video.
you can see his room more clearly due to the better lighting and see that it's the same room as in
>>236815 this video (compare the curtains for example).
also: same boxershorts as in
>>231086 and
>>236793 lol
No. 252791
File: 1487268551638.jpg (42.74 KB, 409x550, dank.jpg)

>>252416his parents are alcoholics so could actually be true
i don't know if that makes it more or less funny
No. 252818
i didnt know he was this ugly. wow. his face is absolutely busted and he has an average chubby body with uneven gyno
LOL life must suck
No. 252846
File: 1487274858385.jpg (103.72 KB, 800x600, 1487271990745.jpg)

Someone just posted this compilation one /r9k/
I thought it was pretty good
(btw if you are reading this: reach out to the Skype in the pastebin)
No. 303646
wow, I knew this guy in high school. he was super skinny and awkward, and he laughed at things that only he found funny. in the classes I had with him, he would usually read or draw, obviously not paying attention, and would chuckle to himself. he made everyone uncomfortable. he always acted like he was smarter than everyone else, but would lose every actual argument he had with teachers or even other students, then would get upset and pout. he also got bullied a little because he was like the resident weirdo, but he tried wearing a trench coat to school one day (and got in trouble for it) and people mostly left him alone after that because they didn't want to risk getting columbine'd.
if I can find a yearbook, I'll try and figure out his last name for you guys. I'm pretty sure he was there all four years, so it might not be too hard. he might still be friends with people from the school on facebook.
No. 303825
>>303646If the facebook-profile linked by
>>262279 was his, his name is Oscar Eklöf.
No. 304009
>>304005"Don't use lolcow as a platform for vendettas or "moral crusades". Don't contact people, or their families, or police without an extremely good reason."
Stop it.
No. 316455
File: 1495198632807.jpg (55.06 KB, 415x460, swag.jpg)

No. 316483
File: 1495202057647.jpg (97.28 KB, 680x680, IMG_0782.JPG)

>>316455>>316480Wow, no wonder he keeps using old pics.
No. 316506
>>316455I agree with
>>316480 kek
I'm disappointed, I legit thought he looked like the autistic less hot brother of Zac Efron who they lock in the basement, feeding him a tray of chicken tendies per day which they slide underneath the door. For the last 17 years he has been occupying the family basement clicking away at his windows 95. His only friend is a set of dumbbells. 4 hours a day is spent doing rage sit ups, getting mega ripped, ready to hulk smash his way out the basement while his more handsome, favourable, social butterfly brother prepares for high school musical in the upstairs dining room
> we're breaking freeeeeeee No. 320507
>>317994one skype account he uses a lot is named "username.250" or something like that iirc
>>318104>>318243i don't think it's a toupée; this dude is close to 30 though, he doesn't make the healthiest lifestyle choices andhe can't really afford one from what it seems like (and his genetics probably aren't favorable for him on that one)
>>316455i pressume the logo in this picture is from the place where he works at; he work at some car repair shop
No. 321511
File: 1495740497698.jpg (339.39 KB, 1131x636, car.jpg)

No. 771954
File: 1548479555454.png (292.45 KB, 714x400, f21d13214a26532fd94aa9bd3c0170…)

>ITT
No. 775099
File: 1549322723738.jpg (47.06 KB, 424x500, 48c8a69dfa5b51462f7f671c62d397…)

>>775082>this guy is still doing his roundsThis predator isn't going to stop any time soon! Not shocked!